算法-查找排序TOPK

1. 查找

1 二分查找(简单)

package main

import "fmt"

func search(nums []int, target int) int {
	left := 0
	right := len(nums) - 1

	for left <= right { // 这里是小于等于
		mid := (left + right) / 2
		if nums[mid] > target {
			right = mid - 1
		} else if nums[mid] < target {
			left = mid + 1
		} else {
			return mid
		}
	}
	return -1 // 找不到 return -1
}

func main() {
	arr := []int{1, 3, 11, 150, 201, 800}
	fmt.Println(search(arr, 11)) // 2(下标)
}

头脑风暴：

1. 一个循环搞定
2. 先判断小于等于

2. 排序

1 快速排序🔥

• https://www.liuvv.com/p/ff8068c0.html

• https://leetcode-cn.com/problems/sort-an-array/

  package main
  
  import "fmt"
  
  func main() {
  	arr := []int{2, 1, 3, 11, 11, 33, 201, 150}
  	fmt.Println("origin", arr)
  	QuickSort(arr, 0, len(arr)-1)
  	fmt.Println("sort", arr)
  }
  
  func QuickSort(arr []int, left int, right int) {
  	if left < right {
  		partIndex := PartIndex(arr, left, right)
  		QuickSort(arr, left, partIndex-1)
  		QuickSort(arr, partIndex+1, right)
  	}
  }
  
  func PartIndex(arr []int, left int, right int) int {
  	base := arr[left]
  	baseIndex := left
  
  	for left < right { // 1. 两个大循环
  		for left < right && arr[right] >= base { // 2. 右边先走，大于等于
  			right--
  		}
  		for left < right && arr[left] <= base { // 3. 左边再走，小于等于
  			left++
  		}
  		arr[left], arr[right] = arr[right], arr[left] // 4. 开始交换
  	}
  
  	arr[baseIndex], arr[left] = arr[left], arr[baseIndex] // 5. 最后和基数交换
  
  	return left
  }
  
  //origin [2 1 3 11 11 33 201 150]
  //sort [1 2 3 11 11 33 150 201]

  头脑风暴：

  1. 里面循环套循环
  2. 先判断小于
  3. 停止相遇要交换

2 堆排序

• https://www.bilibili.com/video/BV1Eb41147dK
• https://www.bilibili.com/video/BV1fp4y1D7cj

堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。大顶堆通常被用来进行”升序”排序，而小顶堆通常被用来进行”降序”排序。

1. 先维护堆性质的函数

与自己的孩子交换，交换后递归交换。

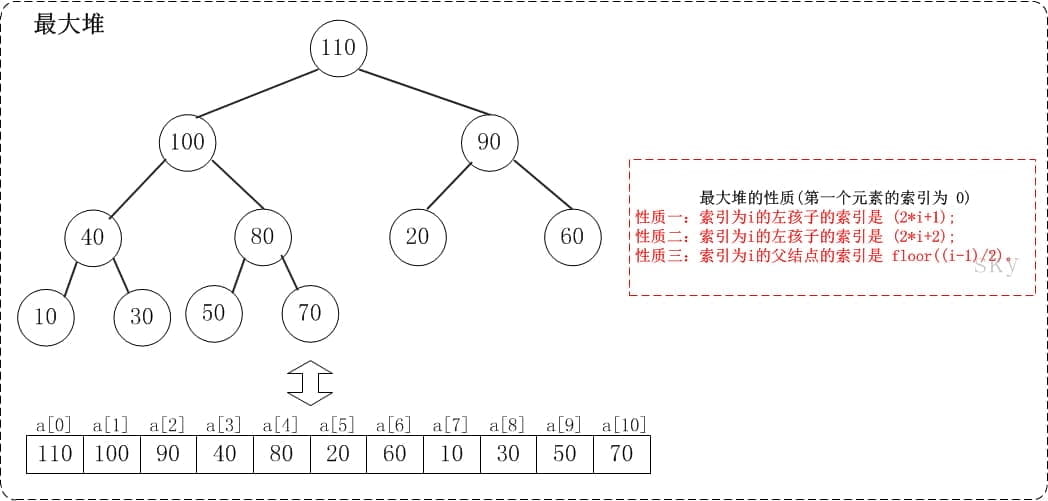
2. 再构建大顶堆

将待排序的序列建成大根堆。

需要有维护堆性质的函数，从后往前调用构建堆就可以了。

3. 不停交换达到堆排序

1. 我们将堆顶其与末尾元素交换，使末尾元素为最大值，然后再调整堆顶元素使得剩下的 n−1 个元素仍为大根堆

2. 再重复 2 的操作我们即能得到一个有序的序列。

package main

import "fmt"

// 1. 维护堆的性质
func heapify(arr []int, length int, index int) {
	maxIndex := index
	lChildIndex := 2*index + 1
	rChildIndex := 2*index + 2

	if lChildIndex < length && arr[lChildIndex] > arr[maxIndex] {
		maxIndex = lChildIndex
	}
	if rChildIndex < length && arr[rChildIndex] > arr[maxIndex] {
		maxIndex = rChildIndex
	}
	if maxIndex != index { // 说明孩子有比自己大的
		arr[maxIndex], arr[index] = arr[index], arr[maxIndex]
		heapify(arr, length, maxIndex)
	}
}

func main() {
	arr := []int{2, 1, 10, 9, 10, 88, 17}
	fmt.Println("origin", arr) //[2 1 10 9 10 88 17]

	// 2. 构建大顶堆
	length := len(arr)
	for i := (length - 1) / 2; i >= 0; i-- {
		heapify(arr, length, i)
	}
	fmt.Println("heap", arr) // [88 10 17 9 1 10 2]

	// 3. 堆排序，切腿，用的是一个方法
	for i := length - 1; i >= 0; i-- {
		arr[i], arr[0] = arr[0], arr[i]
		heapify(arr, i, 0)
	}
	fmt.Println("heap_sort", arr) // [1 2 9 10 10 17 88]
}

/*
1. 构建大顶堆，倒着构建
2. 然后堆排序，倒着构建，切腿，再次构建大顶堆
*/

3 TopK

参考堆排序代码，先建堆。

1. topK

用小顶堆

package main

import "fmt"

func heapify(arr []int, index int, length int) {
	minIndex := index
	lChildIndex := 2*index + 1
	rChildIndex := 2*index + 2
	if lChildIndex < length && arr[lChildIndex] < arr[minIndex] {
		minIndex = lChildIndex
	}
	if rChildIndex < length && arr[rChildIndex] < arr[minIndex] {
		minIndex = rChildIndex
	}
	if minIndex != index {
		arr[minIndex], arr[index] = arr[index], arr[minIndex]
		heapify(arr, minIndex, length)
	}
}

func main() {
	topK := 3
	var arr = []int{10, 9, 111, 30, 19, 1}
	// 建堆
	for i := topK; i >= 0; i-- {
		heapify(arr, i, topK)
	}

	// 维护堆
	for i := topK; i < len(arr); i++ {
		if arr[i] > arr[0] {
			arr[i], arr[0] = arr[0], arr[i]
			heapify(arr, 0, topK)
		}
	}
	fmt.Println(arr)
}

2 最小的k个数(简单) 最小K个数(中等)

使用大顶堆，和堆顶比较，堆顶大就直接换掉，接下来这个堆就是数字最小的大顶堆。

package main

import "fmt"

// 建堆
func buildHeap(arr []int, size int) {
	for i := size / 2; i >= 0; i-- {
		heapify(arr, i, size)
	}
}

// 维护堆
func heapify(arr []int, index int, length int) {
	l := index*2 + 1
	r := index*2 + 2

	maxIndex := index
	if l < length && arr[l] > arr[maxIndex] {
		maxIndex = l
	}
	if r < length && arr[r] > arr[maxIndex] {
		maxIndex = r
	}

	if maxIndex != index {
		arr[maxIndex], arr[index] = arr[index], arr[maxIndex]
		heapify(arr, maxIndex, length)
	}
}

func getLeastNumbers(arr []int, k int) []int {

	buildHeap(arr, k)

	for i := k; i < len(arr); i++ {
		if arr[i] < arr[0] {
			arr[i], arr[0] = arr[0], arr[i]
			heapify(arr, 0, k)
		}
	}
	var res []int
	for i := 0; i < k; i++ {
		res = append(res, arr[i])
	}
	return res

}

func main() {
	arr := []int{2, 1, 10, 9, 10, 88, 17}
	fmt.Println("least4", getLeastNumbers(arr, 3)) // 9 1 2
	fmt.Println("least2", getLeastNumbers(arr, 2)) // 2 1
}

3 数组中的第K个最大元素(中等)

使用的大顶堆, 需要全入堆

func buildHeap(arr []int, size int) {
	for i := size / 2; i >= 0; i-- {
		heapify(arr, i, size)
	}
}

func heapify(arr []int, index int, length int) {
	l := index*2 + 1
	r := index*2 + 2

	temp := index
	if l < length && arr[l] > arr[temp] {
		temp = l
	}
	if r < length && arr[r] > arr[temp] {
		temp = r
	}

	if temp != index {
		arr[temp], arr[index] = arr[index], arr[temp]
		heapify(arr, temp, length)
	}
}



func findKthLargest(nums []int, k int) int {
	buildHeap(nums, len(nums))

	length := len(nums) - 1
	for i := 0; i < k; i++ {
		nums[0], nums[length] = nums[length], nums[0]
		length--
		heapify(nums, 0, length)
	}
	return nums[len(nums)-k]
}

4. 参考资料

• https://lyl0724.github.io/2020/01/25/1/