复杂度分析主要从「时间」和「空间」两个维度来进行分析。

时间维度顾名思义就是算法需要消耗的时间，「时间复杂度」是常用的分析单位。
空间维度代表算法需要占用的内存空间，我们通常用「空间复杂度」来分析。

1. 时间复杂度

大O符号表示法，既 T(n) = O(f(n))，它表示一个算法的渐进时间复杂度。其中 f(n) 表示代码执行次数之和，O表示正比例关系。我们来看一个例子：

1
2
3

for (int i = 1; i <= n; i++) {
    x++;
}

每个算法需要多少的运行时间呢？我们知道这个for loop有n个循环，假设其中 x++ 计算的消耗是一个单位，那么第一次循环是1单位，第二次循环是2单位，所以整个循环语句就要消耗n个单位。可以发现，消耗的单位时间随着循环的次数而变化，循环次数为1，时间为1单位；循环次数为10，时间为10单位；循环次数为n，时间为n单位。所以这个算法的「时间复杂度」可以表示为：T (n) = O(n)。

有人可能不同意了，因为严格计算下，int i = 1也要消耗1单位时间，i <= n和i++也都需要1单位时间，所以严格来说总时间是 T(n) = 1 + 3n。但是我们依然会简化为n，因为「大O表示法」用与表示计算的增长变化趋势。

在这个例子中，如果n无限大的时候，T(n) = 1 + 3n 中的常数1就没有意义了，倍数3也影响不大。所以简化为 T(n) = O(n) 就可以了。

我们再来看一个例子：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

在外层循环中，i 总共需要n层循环，在每一次内层循环中，j 也会循环n次。如果用「大O表示法」来计算，那么两个循环语句的复杂度就是 O(n²)，如果我们将这两个算法合并到一起：

for (int i = 1; i <= n; i++) {
    x++;
}
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

整个算法复杂度就变为 O(n + n²)，在n无限大的情况下，可以简化为 O(n²)。

1.0 常见的时间复杂度

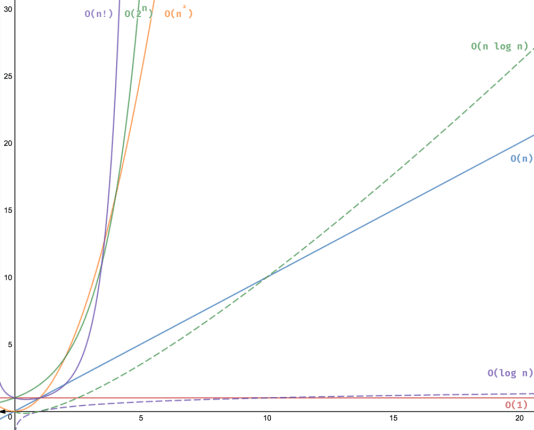
常数阶O(1)
对数阶O(logN)
线性阶O(n)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
K次方阶O(n^k)
指数阶(2^n)
阶乘O(n!)

上面的时间复杂从上到下复杂度越来越大，也意味着执行效率越来越低。

1.1 常数阶O(1)

访问数组中的某个元素。例如，arr[i]。

1.2 对数阶O(logN) 【二分查找】

二分查找。每次查找都将问题规模减半。

1.3 线性阶O(n) 【循环】

遍历一个长度为n的数组。例如，计算数组元素之和。

1.4 线性对数阶O(nlogN) 【快速排序】

快速排序、归并排序等。它们的最优和平均时间复杂度都是O(n log n)。

for(int i = 0; i <= n: i++) {
    int x = 1;
    while(x < n) {
        x = x * 2;
    }
}

因为每次循环的复杂度为O(logN)，所以n * logN = O(nlogN)

1.5 平方阶O(n²) 【冒泡排序】

冒泡排序、选择排序、插入排序。在这些算法中，存在嵌套的循环。

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

1.6 指数阶O(2^n) 【汉诺塔】

解决汉诺塔问题的递归算法。每次递归调用都会产生两个新的递归调用。

1.7 阶乘O(n!)

求解旅行商问题的暴力法。需要计算所有可能的路径。

2. 空间复杂度

「空间复杂度」反映的则是内存空间增长的趋势，不是用来计算程序具体占用的空间。

比较常用的空间复杂度有：O(1)、O(n)、O(n²)。

2.1 O(1) 常数空间复杂度

使用有限数量的额外变量，例如交换两个变量的值。

2.2 O(n) 线性空间复杂度

使用一个额外数组来存储输入数据，例如创建一个副本数组。

func copyArray(arr []int) []int {
    n := len(arr)
    copy := make([]int, n)
    for i := range arr {
        copy[i] = arr[i]
    }
    return copy
}

2.3 O(n²) 二次空间复杂度

创建一个二维矩阵，例如动态规划中的二维数组。dp 数组是一个大小为 (m+1) x (n+1) 的二维数组，所以空间复杂度是 O(mn)。

func longestCommonSubsequence(X, Y string) int {
    m, n := len(X), len(Y)
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }

    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            if X[i-1] == Y[j-1] {
                dp[i][j] = dp[i-1][j-1] + 1
            } else {
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
            }
        }
    }
    return dp[m][n]
}

3. 复杂度速查表

3.1 数据结构

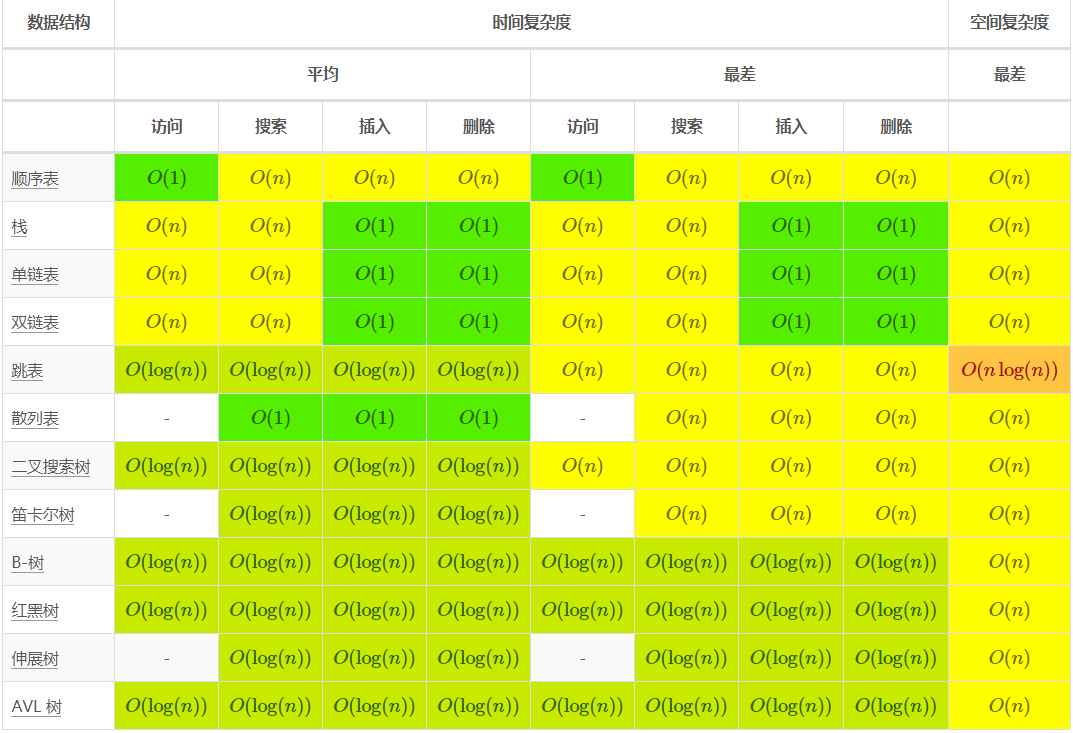
3.2 数组排序

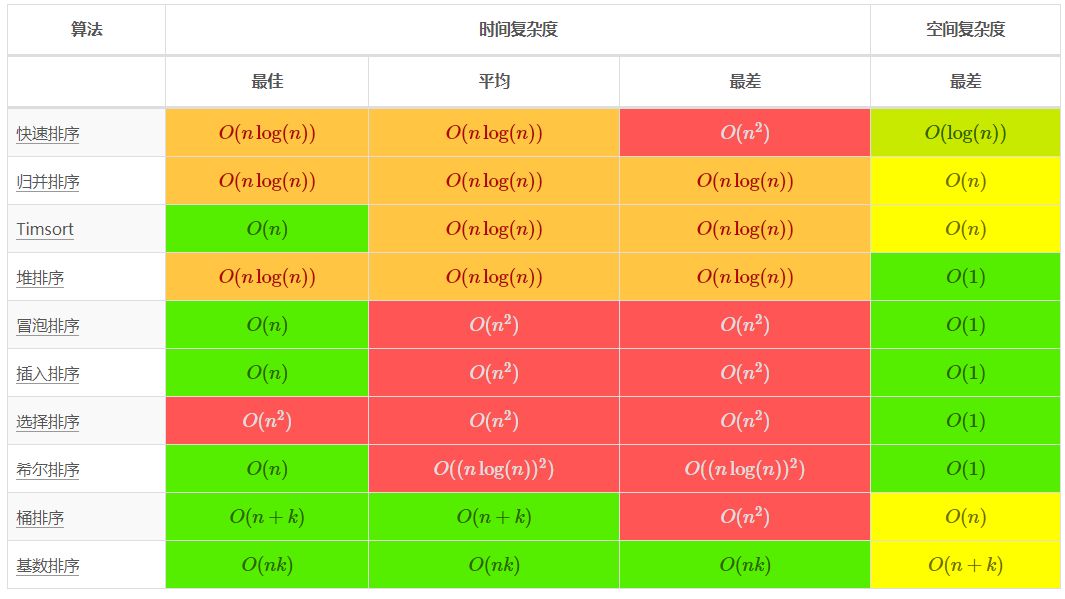
冒泡、选择、插入排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O(n²)）（一遍找元素O(n)，一遍找位置O(n)）

快速、归并、希尔、堆基于二分思想，log以2为底，平均时间复杂度为O(nlogn)（一遍找元素O(n)，一遍找位置O(logn)）

3.3 堆

建堆的时间复杂度是O(n)；
堆的插入、删除元素的时间复杂度都是O(log n)；
堆排序的时间复杂度是O(nlog n)；
堆排序的空间复杂度是O(1)；

Levon's Blog

算法复杂度的理解